用什么优化算法(遗传算法, 神经网络等)解决多个参数的优化问题?
约10个参数会影响结果,每个参数的取值1-10。这些参数共同决定输出结果(最好结果是1.0)。用什么优化算法(遗传算法, 神经网络等)能快速地解决这些参数的优化问题?
机器学习的优化(目标),简单来说是:搜索模型的一组参数 w,它能显著地降低代价函数 J(w),该代价函数通常包括整个训练集上的性能评估(经验风险)和额外的正则化(结构风险)。与传统优化不同,它不是简单地根据数据的求解最优解,在大多数机器学习问题中,我们关注的是测试集(未知数据)上性能度量P的优化。
- 对于模型测试集是未知,我们只能通过优化训练集的性能度量P_train,在独立同分布基础假设下,期望测试集也有较好的性能(泛化效果),这意味并不是一味追求训练集的最优解。
- 另外,有些情况性能度量P(比如分类误差f1-score)并不能高效地优化,在这种情况下,我们通常会优化替代损失函数 (surrogate loss function)。例如,负对数似然通常用作 0 ? 1 分类损失的替代。
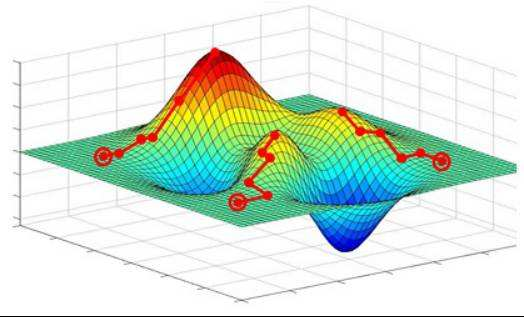
当我们机器学习的学习目标是极大化降低(经验)损失函数,这点和传统的优化是比较相似的,那么如何实现这个目标呢?我们第一反应可能是直接求解损失函数最小值的公式/解析解(如最小二乘法),获得最优的模型参数。但是,通常机器学习模型的损失函数较复杂,很难直接求最优解。幸运的是,我们还可以通过优化算法(如遗传算法、梯度下降算法、牛顿法等)有限次迭代优化模型参数,以尽可能降低损失函数的值,得到较优的参数值(数值解)。上述去搜索一组最\\较优参数解w所使用的算法,即是优化算法。下图优化算法的总结:(图与本文内容较相符,摘自@teekee)

最小二乘法常用在机器学习回归模型求解析解(对于复杂的深度神经网络无法通过这方法求解),其几何意义是高维空间中的一个向量在低维子空间的投影。
如下以一元线性回归用最小二乘法求解为例。

其损失函数mse为:

对损失函数求极小值,也就是一阶导数为0。通过偏导可得关于参数a及偏置b的方程组:

代入数值求解上述线性方程组,可以求解出a,b的参数值。也就是求解出上图拟合的那条直线ax+b。
注:神经网络优化算法以梯度下降类算法较为高效,也是主流的算法。而遗传算法、贪心算法、模拟退火等优化算法用的比较少。
遗传算法(Genetic Algorithms,GA)是模拟自然界遗传和生物进化论而成的一种并行随机搜索最优化方法。与自然界中“优胜略汰,适者生存”的生物进化原理相似,遗传算法就是在引入优化参数形成的编码串联群体中,按照所选择的适应度函数并通过遗传中的选择、交叉和变异对个体进行筛选,使适应度好的个体被保留,适应度差的个体被淘汰,新的群体既继承了上一代的信息,又优于上一代。这样反复循环迭代,直至满足条件。
梯度下降算法可以直观理解成一个下山的方法,将损失函数J(w)比喻成一座山,我们的目标是到达这座山的山脚(即求解出最优模型参数w使得损失函数为最小值)。

下山要做的无非就是“往下坡的方向走,走一步算一步”,而在损失函数这座山上,每一位置的下坡的方向也就是它的负梯度方向(直白点,也就是山的斜向下的方向)。在每往下走到一个位置的时候,求解当前位置的梯度,向这一步所在位置沿着最陡峭最易下山的位置再走一步。这样一步步地走下去,一直走到觉得我们已经到了山脚。 当然这样走下去,有可能我们不是走到山脚(全局最优,Global cost minimun),而是到了某一个的小山谷(局部最优,Local cost minimun),这也后面梯度下降算法的可进一步调优的地方。 对应的算法步骤,直接截我之前的图:

梯度下降是一个大类,常见的梯度下降算法及优缺点,如下图:

对于深度学习而言“随机梯度下降, SGD”,其实就是基于小批量(mini-batch)的随机梯度下降,当batchsize为1也就是在线学习优化。
随机梯度下降是在梯度下降算法效率上做了优化,不使用全量样本计算当前的梯度,而是使用小批量(mini-batch)样本来估计梯度,大大提高了效率。原因在于使用更多样本来估计梯度的方法的收益是低于线性的,对于大多数优化算法基于梯度下降,如果每一步中计算梯度的时间大大缩短,则它们会更快收敛。且训练集通常存在冗余,大量样本都对梯度做出了非常相似的贡献。此时基于小批量样本估计梯度的策略也能够计算正确的梯度,但是节省了大量时间。
对于mini-batch的batchsize的选择是为了在内存效率(时间)和内存容量(空间)之间寻找最佳平衡。
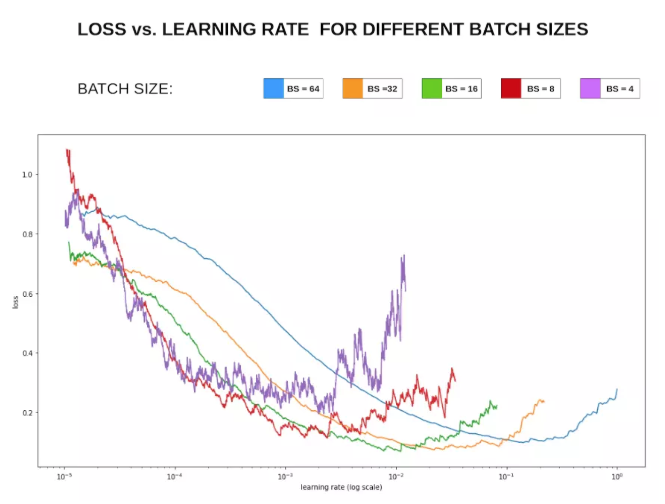
- batchsize 不能太大。 较大的batch可能会使得训练更快,但可能导致泛化能力下降。更大的batch size 只需要更少的迭代步数就可以使得训练误差收敛,还可以利用大规模数据并行的优势。但是更大的batch size 计算的梯度估计更精确,它带来更小的梯度噪声。此时噪声的力量太小,不足以将参数带出一个尖锐极小值的吸引区域。这种情况需要提高学习率,减小batch size 提高梯度噪声的贡献。
- batchsize不能太小。 小的batchsize可以提供类似正则化效果的梯度噪声,有更好的泛化能力。但对于多核架构来讲,太小的batch并不会相应地减少计算时间(考虑到多核之间的同步开销)。另外太小batchsize,梯度估计值的方差非常大,因此需要非常小的学习速率以维持稳定性。如果学习速率过大,则导致步长的变化剧烈。
还可以自适应调节batchsize,参见《Small Batch or Large Batch? Peifeng Yin》
Momentum算法在梯度下降中加入了物理中的动量的概念,模拟物体运动时候的惯性,即在更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度对之前的梯度进行微调,这样一来,可以在一定程度上增加稳定性,从而学习的更快,并且有一定的摆脱局部最优的能力。
该算法引入了变量 v 作为参数在参数空间中持续移动的速度向量,速度一般可以设置为负梯度的指数衰减滑动平均值。对于一个给定需要最小化的代价函数,动量可以表达为:更新后的梯度=折损系数γ动量项+ 学习率?当前的梯度。

其中 ? 为学习率,γ ∈ (0, 1]为动量系数,v 是速度向量。一般来说,梯度下降算法下降的方向为局部最速的方向(数学上称为最速下降法),它的下降方向在每一个下降点一定与对应等高线的切线垂直,因此这也就导致了 GD 算法的锯齿现象。加入动量法的梯度下降是令梯度直接指向最优解的策略之一。

Nesterov动量是动量方法的变种,也称作Nesterov Accelerated Gradient(NAG)。在预测参数下一次的位置之前,我们已有当前的参数和动量项,先用(θ?γvt?1)下一次出现位置的预测值作为参数,虽然不准确,但是大体方向是对的,之后用我们预测到的下一时刻的值来求偏导,让优化器高效的前进并收敛。

在平滑的凸函数的优化中,对比批量梯度下降,NAG 的收敛速度超出 1/k 到 1/(k^2)
Adagrad 亦称为自适应梯度(adaptive gradient),允许学习率基于参数进行调整,而不需要在学习过程中人为调整学习率。Adagrad 根据不常用的参数进行较大幅度的学习率更新,根据常用的参数进行较小幅度的学习率更新。然而 Adagrad 的最大问题在于,在某些情况,学习率变得太小,学习率单调下降使得网络停止学习过程。

其中是梯度平方的积累量s,在进行参数更新时,学习速率要除以这个积累量的平方根,其中加上一个很小值是ε为了防止除0的出现。由于s 是逐渐增加的,那么学习速率是相对较快地衰减的。
RMSProp 算是对Adagrad算法的改进,主要是解决学习速率过快衰减的问题,它不是像AdaGrad算法那样暴力直接的累加平方梯度,而是加了一个衰减系数γ 来控制历史信息的获取多少。
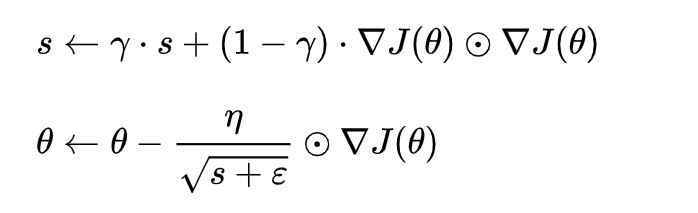
Adam 算法为两种随机梯度下降的优点集合:
- 适应性梯度算法(AdaGrad)为每一个参数保留一个学习率以提升在稀疏梯度(即自然语言和计算机视觉问题)上的性能。
- 均方根传播(RMSProp)基于权重梯度最近量级的均值为每一个参数适应性地保留学习率。这意味着算法在非稳态和在线问题上有很有优秀的性能。
Adam 算法同时获得了 AdaGrad 和 RMSProp 算法的优点,像RMSprop 一样存储了过去梯度的平方 v的指数衰减平均值 ,也像 momentum 一样保持了过去梯度 m 的指数衰减平均值:

如果 m 和 v被初始化为 0 向量,那它们就会向 0 偏置,所以做了偏差校正放大它们:

梯度更新能够从梯度均值及梯度平方两个角度进行自适应地调节,而不是直接由当前梯度决定。

牛顿法和梯度下降法相比,两者都是迭代求解,不过梯度下降法是梯度求解(一阶优化),而牛顿法是用二阶的海森矩阵的逆矩阵求解。相对而言,使用牛顿法收敛更快(迭代更少次数),但是每次迭代的时间比梯度下降法长(计算开销更大,实际常用拟牛顿法替代)。

通俗来讲,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,后面坡度是否会变得更大。所以,可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部。但是,牛顿法对初始值有一定要求,在非凸优化问题中(如神经网络训练),牛顿法很容易陷入鞍点(牛顿法步长会越来越小),而梯度下降法则更容易逃离鞍点(因此在神经网络训练中一般使用梯度下降法,高维空间的神经网络中存在大量鞍点)。
综上, 对于神经网络的优化,常用梯度下降等较为高效的方法。梯度下降算法类有SGD、Momentum、Adam等算法可选。对于大多数任务而言,通常可以直接先试下Adam,然后可以继续在具体任务上验证不同优化器效果。
文章首发公众号“算法进阶”,更多原创文章敬请关注 个人github:https://github.com/aialgorithm
遗传算法采用“优胜劣汰,适者生存”的生物进化原理,按照所选择的适应度函数并通过遗传中的复制、交叉、变异对个体进行筛选,适应度高的被留下来,组成新的群体。
它主要包括三个方面:(1)复制:从一个旧群体中选择适应度高的在下一代中更可能被保留下来。 (2)交叉 :通过两个个体的交换组合,产生新的优良品种。交叉又有单点交叉、两点交叉、一致交叉、顺序交叉和周期交叉,其中单点交叉运用最广。单点交叉:任意选择两个染色体,随机选择一个交换点位置,交换两个染色体右边的部分。 (3)变异:变异运算用来模拟生物在自然的遗传环境中因为各种偶然因素引起的基因突变。算法中以很小的概率随机改变(染色体某一位置)的值,表现为随机将某一基因1变为0,0变为1。
算法流程为:初始化群体---->计算各个个体的适应度---->根据适应度选择个体(适应度高的留下,适应度低的淘汰)----->按照一定的概率进行交叉、变异来产生新的优良品种----->形成新的群体计算适应度(迭代)----->满足终止条件,输出结果
算法特点:(1)直接对结构对象进行操作 (2)具有隐含并行性和更好的全局寻优能力 (3)能自动获取和指导优化的搜索空间,自适应调整方向,不需要确定的规则
2、模拟退火算法
它采用类似于物理退火的过程,先在一个高温状态下,逐渐退火,在每个温度下进行状态转移,最终达到物理基态。
模拟退火算法从某一高温出发,以预设的领域函数,产生新的状态。比较新旧状态下的能量,如果新状态能量小于旧状态,则状态发生变化。否则,以Metropolis接受准则发生变化。当状态稳定后便可以开始降温,在下一温度继续迭代。
Metropolis准则:温度为T,当前状态i,新状态j,若Ei>Ej,则接受j为当前状态;否则,计算状态j与状态i的比值,若大于[0,1)产生的随机数,则接受j为当前状态。它以概率形式接受新状态,避免局部最优。
领域函数:通常在当前状态的领域结构以一定概率方式产生,概率分布可以是均匀分布、正态分布、指数分布等。
该算法的核心主要是内外两次循环,内循环模拟同一温度下多次的状态转移,外循环为进行的迭代次数。
该算法的初始温度和终止温度过低或过高都会延长搜索时间,而降温太快又容易漏掉全局最优,因此要选择合适的冷却进度表。
模拟退火算法它主要是在每一次的迭代下,寻找这次迭代的最优解(局部搜索,当前状态和下一状态进行比较),然后模拟降温过程进行迭代。若是降温的越慢,得到的最优解更精确,但搜索时间过长。由于计算速度和时间限制,在优化效果和计算时间上存在矛盾,优化效果不理想。
遗传算法它可以进行多个个体同时比较,有潜在的并行性。但是他得三个算子的实现有参数(如交叉和变异的概率),参数的选择大多依靠经验,它可能会影响效果。
3、粒子群算法
粒子群算法通过更新每次迭代的局部最优和全局最优来更新粒子的速度和位置,它保留了全局和局部,对于较快收敛和避免过早陷入局部最优都有较好的效果。
粒子群算法和遗传算法都可以同时比较多个个体寻找最优解,不同的是粒子群算法的每个个体还要和过去的个体进行比较,而遗传算法是把适应度大的较大概率的保留到下一代中,适应度小的淘汰。模拟退火算法它是对单个个体温度不变下,状态转移,求目标函数值更新最优解,随着温度不断降低,状态转移的范围也逐渐变小。
//遗传算法
import numpy as np
DNA_size=10
pops=60
jiaohuan=0.7
bianyi=0.003
gen=100
x_bound=[-3,3]
y_bound=[-3,3]
def fun(x,y):
return 100.0*(y-x**2.0)**2.0+(1-x)**2.0
def get_fitness(pop):
x,y=trans(pop)
pred=fun(x,y)
return pred
def trans(pop):
x_pop=pop[:,0:DNA_size]
y_pop=pop[:,0:DNA_size]
x=x_pop.dot(2**np.arange(DNA_size)[::-1])/float(2**DNA_size -1)*(x_bound[1]-x_bound[0])+x_bound[0]
y=y_pop.dot(2**np.arange(DNA_size)[::-1])/float(2**DNA_size-1)*(x_bound[1]-x_bound[0])+x_bound[0]
return x,y
def crossover(pop):
new_pop=[]
pred=get_fitness(pop)
index=np.argmax(pred)
index2=np.argmin(pred)
for father in pop:
if (father == pop[index2]).all()==True:
child=pop[index]
else:
child=father
if np.random.rand()<jiaohuan:
mother=pop[np.random.randint(pops)]
cross_point=np.random.randint(low=0,high=DNA_size*2)
child[cross_point:]=mother[cross_point:]
child=mutation(child)
new_pop.append(child)
return new_pop
def mutation(child):
if np.random.rand()<bianyi :
mutate_point=np.random.randint(0,DNA_size)
child[mutate_point]=child[mutate_point]^1
return child
def select(pop,fitness):
idx=np.random.choice(np.arange(pops),size=pops,replace=True,p=(fitness)/(fitness.sum()))
return pop[idx]
def print_info(pop):
fitness=get_fitness(pop)
max_index=np.argmax(fitness)
print("最优解:",fitness[max_index])
x,y=trans(pop)
print("最优基因型:",pop[max_index])
print("最优解的x,y :",x[max_index],y[max_index])
if __name__=="__main__":
pop=np.random.randint(2,size=(pops,DNA_size*2))
fitness=get_fitness(pop)
for i in range(gen):
pop=np.array(crossover(pop))
fitness=get_fitness(pop)
pop=select(pop,fitness)
print_info(pop)//模拟退火算法
import numpy as np
import matplotlib.pyplot as plt
import math
def fun(x):
y=x**3-60*x**2-4*x+6
return y
T=1000
Tmin=10
x=np.random.uniform(low=0,high=100)
k=50
t=0
y=0
while T>=Tmin:
for i in range(k):
y=fun(x)
xnew=x+np.random.uniform(low=-0.055,high=0.055)*T
if (0<=xnew and xnew<=100):
ynew=fun(xnew)
if ynew-y<0:
x=xnew
else:
p=math.exp(-(ynew-y)/T)
r=np.random.uniform(low=0,high=1)
if r<p:
x=xnew
t +=1
print(t)
T=1000/(1+t)
print(x, fun(x))
//粒子群算法
import numpy as np
import matplotlib.pyplot as plt
class PSO(object):
def __init__(self, population_size, max_steps):
self.w = 0.6 # 惯性权重
self.c1 = self.c2 = 2
self.population_size = population_size # 粒子群数量
self.dim = 2 # 搜索空间的维度
self.max_steps = max_steps # 迭代次数
self.x_bound = [-10, 10] # 解空间范围
self.x = np.random.uniform(self.x_bound[0], self.x_bound[1],
(self.population_size, self.dim)) # 初始化粒子群位置
self.v = np.random.rand(self.population_size, self.dim) # 初始化粒子群速度
fitness = self.calculate_fitness(self.x)
self.p = self.x # 个体的最佳位置
self.pg = self.x[np.argmin(fitness)] # 全局最佳位置
self.individual_best_fitness = fitness # 个体的最优适应度
self.global_best_fitness = np.min(fitness) # 全局最佳适应度
def calculate_fitness(self, x):
return np.sum(np.square(x), axis=1)
def evolve(self):
fig = plt.figure()
for step in range(self.max_steps):
r1 = np.random.rand(self.population_size, self.dim)
r2 = np.random.rand(self.population_size, self.dim)
# 更新速度和权重
self.v = self.w*self.v+self.c1*r1*(self.p-self.x)+self.c2*r2*(self.pg-self.x)
self.x = self.v + self.x
plt.clf()
plt.scatter(self.x[:, 0], self.x[:, 1], s=30, color='k')
plt.xlim(self.x_bound[0], self.x_bound[1])
plt.ylim(self.x_bound[0], self.x_bound[1])
plt.pause(0.1)
fitness = self.calculate_fitness(self.x)
# 需要更新的个体
update_id = np.greater(self.individual_best_fitness, fitness)
self.p[update_id] = self.x[update_id]
self.individual_best_fitness[update_id] = fitness[update_id]
# 新一代出现了更小的fitness,所以更新全局最优fitness和位置
if np.min(fitness) < self.global_best_fitness:
self.pg = self.x[np.argmin(fitness)]
self.global_best_fitness = np.min(fitness)
print('step: %.d, best fitness: %.5f, mean fitness: %.5f' % (step+1, self.global_best_fitness, np.mean(fitness)))
pso = PSO(100, 100)
pso.evolve()
plt.title("minimum sum square")
plt.show()当前人工智能领域的先进技术层出不穷,诸如计算机视觉、自然语言处理、影像生成,深度神经网络等先进技术日新月异。然而,从计算能力、内存或能源消耗角度来看,这些新技术的成本可能令人望而却步,其中某些成本对于大多数硬件资源受限的用户来说,则完全负担不起。所以说,人工智能许多领域将对神经网络进行必要的修剪,在确保其性能的同时降低其运行成本。
这就是神经网络压缩的全部要点,在这一领域,有多种方法来实现神经网络的压缩,如量化、分解蒸馏等等,本文的重点在于阐述神经网络的剪枝。
神经网络剪枝旨在去除性能良好但花费大量资源的多余部分网络。尽管大型神经网络的学习能力有目共睹,但事实上,在训练过程结束后,并不是所有的神经网络全部有用,神经网络剪枝的想法便是在不影响网络性能的情况下去除这些无用的部分。
在这个研究领域,每年均有几十篇,甚至数百篇论文发布,众多的论文揭示了这一想法蕴含的复杂性。通过阅读这些文献,可以快速识别出神经网络的无用部分,并在训练前后去除它们,值得强调的是,并不是所有的修剪都可以提速神经网络,某些工作甚至会事倍功半。
本文在阅读原生神经剪枝论文的基础上,提出了解决神经网络修剪的解决方案,依次回答了三个这一领域中的核心问题:“应该对哪部分进行修剪?”、“如何判断哪些部分可以修剪?”以及“如何在不损害网络的情况下进行修剪?”。综上所述,本文将详细介绍神经网络剪枝的结构、剪枝准则和剪枝方法。
当涉及神经网络的成本时,参数的数目和FLOPS(每秒钟的浮点操作次数)是其中最广泛使用的指标之一。看到网络显示出天文数字的参数(对某些人来说会花费高达数十亿美元的成本),这的确令人生畏。通过直接删除参数,从而直观地减少参数数目,这一方法肯定有效。实际上,这一方法在多个文献中均有提及,修剪参数是文献中提到的应用最为广泛的示例,被视为处理剪枝时的默认框架。
直接修剪参数的方法有诸多优点。首先,它很简单,在参数张量内,将其权重值设为零,便可以实现对参数的修剪。在Pytorch深度学习框架中,可以轻松地访问到网络的所有参数,实现起来非常简单。尽管如此,修剪参数的最大优势是:它们是网络中最小、最基本的元素,因此,只要数量足够多,便可以在不影响性能的情况下,对它们进行大量修剪。这种精细修剪的粒度使得可以在非常精密的模式下实现剪枝,例如,可以对卷积内核内的参数进行修剪。由于剪枝权值根本不受任何约束条件的限制,而且是修剪网络的最好方法,因此将这种方式称为非结构化剪枝。
然而,这种方法的致命缺点是:大多数深度学习框架和硬件无法加速稀疏矩阵的计算,这意味着无论你为参数张量填充多少个零,都不会对实际训练成本产生实质的影响,仅仅是一种直接改变网络架构的方式进行剪枝,而不是对任何框架都放之四海而皆准的方法。
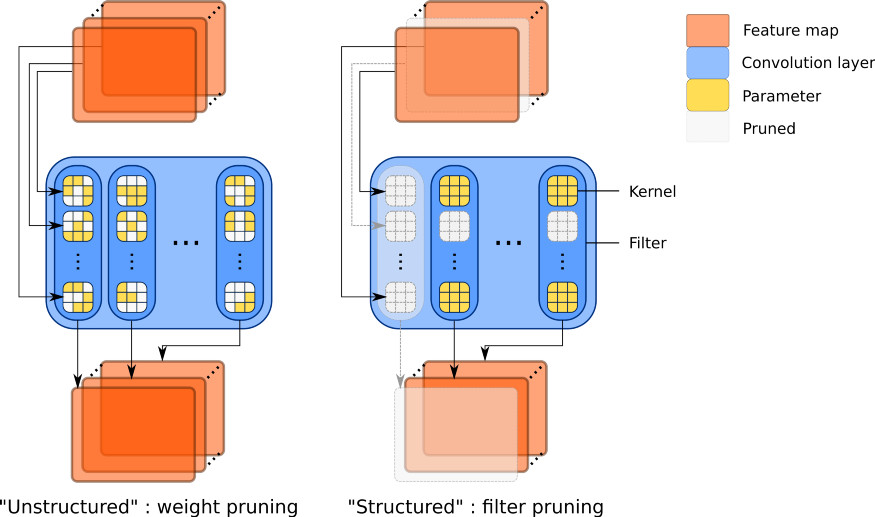
非结构化(左)和结构化(右)剪枝之间的区别:结构化剪枝会同时删除卷积过滤器和内核行,而不仅仅是修剪参数。从而使得中间特征映射的数目更少。
结构化剪枝专注于对更为庞大的结构进行修剪,比如修剪整个神经元,或者,在更现代的深度卷积网络中,直接修剪卷积过滤器。大型网络往往包含许多卷积层,每个层中包含数百或数千个过滤器,可以对卷积层过滤器进行细粒度的修剪。移除这种结构不仅使得深度神经网络的层结构更为稀疏,而且这样做还可以去除过滤器输出的特性映射。
由于减少了参数,这种网络不仅存储起来更为轻便,而且计算量也得以降低,生成更为便捷的中间表示,因此在运行时需要更少的内存。实际上,有时降低带宽比减少参数数目更有益。对于涉及大型图像的任务,如语义分割或对象检测,中间表示可能比网络本身更加消耗内存,出于这些原因,可以将过滤器修剪视为默认的结构化剪枝。
在应用结构化剪枝时,应注意以下几方面:首先,应考虑如何构建卷积层,对于Cin输入通道和Cout输出通道,卷积层由Cout过滤器构成,过滤器分别对Cin内核进行计算;每个过滤器均输出一个特征映射,每个输入通道为一个内核专用。基于这种架构,卷积网络为堆叠的多个卷积层,当对整个过滤器进行剪枝时,可以观察到对每一个过滤器剪枝的过程,随后输出特征映射,这一过程也会导致对后续层内核的修剪。这意味着,当修剪过滤器时,在第一次删除参数之后,实际删除的参数数量是最初认为要删除的参数数量的数倍。
下面来考虑一下这种特殊情况,当一不留神把所有卷积层都修剪掉之后(虽然卷积层被修剪掉了,但神经网络并没有被摧毁,这由神经网络的架构来决定),无法链接到前一层的输出,这也可以是神经网络的一种剪枝方式:修剪掉所有卷积层,实际上等于修剪掉了所有上一层的输出,所以只能连接到其他地方(如残余连接或并行通道)。
在对过滤器剪枝时,首先应该计算出实际参数的确切数量,再根据过滤器在神经网络架构中的分布,修剪相同数量的过滤器,如果实际参数的数量与修剪参数数量不同,结果将不具备可比性。
在进入下一个主题之前,需要提及的是:依然有少数工作集中于剪枝卷积内核、核内架构乃至是特定的参数结构。然而,这些架构需要用特殊的方法来实现(如非结构化剪枝)。此外,另一种方法是对每个核中的某个参数进行修剪,将卷积层转换为“移位层”,这可以通过一次移位操作和一次1×1卷积的组合来实现。

结构化剪枝的缺点:输入和输出维度的改变会引发某些偏差。
在决定了采用何种结构进行剪枝之后,下一个问题便会是:“现在,如何找出保留哪些部分,哪些部分需要修剪?”为了回答这个问题,通过对参数、过滤器或其他特性进行排序基础上,生成一个恰当的剪枝准则。
一个非常直观而又有效的准则是:修剪掉那些权重绝对值最小的参数。事实上,在权重衰减的约束条件下,那些对函数没有显著贡献的参数在训练期间,它们的幅度会不断减小。因此,那些权重比较小的参数便显得多余了。原理很简单,这一准则在当前神经网络的训练中被广泛使用,已成为该领域的主角。
尽管这个准则在非结构化剪枝的实现中显得微不足道,但大家更想知道如何将其应用于结构化剪枝。一种简单的方法是根据过滤器的范数(例如L1或L2)对过滤器进行排序。这种方法实现起来简单粗暴,即将多个参数封装在一起:例如,将卷积过滤器的偏差和批归一化参数封装到一起,将在并行层的过滤器输出融合起来,从而减少通道数目。
其中一种方法是:在无需计算所有参数的组合范数的前提下,为需要修剪的每一层的特征映射插入一个可学习的乘法因子,当它减少为零时,有效地删除负责这个通道的所有参数集,该方法可用于修剪权重幅度较小的参数。
权重大小剪枝准则并非唯一流行的准则,实际上,还有另一个重要准则,即梯度大小剪枝准则,也非常适用。根据上世纪80年代的一些基础理论,通过泰勒分解去消除参数对损失的影响,某些指标:如反向传播的梯度,可提供一个不错的判断方法,来确定在不损害网络的情况下可以修剪掉哪些参数。
在实际项目中,这一准则是这样实现的:首先计算出小批量训练数据的累积梯度,再根据这个梯度和每个参数对应权重之间的乘积进行修剪。
最后一个需要考虑的因素是,所选择的剪枝准则是否适用于网络的所有参数或过滤器,还是为每一层独立计算而设计。虽然神经网络全局剪枝可以生成更优的结果,但它会导致层垮塌。避免这个问题的简单方法是,当所使用的全局剪枝方法无法防止层垮塌时,就采用逐层的局部剪枝。

局部剪枝(左)和全局剪枝(右)的区别:局部剪枝对每一层分别进行剪枝,而全局剪枝同时将其应用于整个网络
在明确了剪枝结构和剪枝准则之后,剩下就是应该使用哪种方法来剪枝一个神经网络。这实际上是最令人困惑的话题,因为每一篇论文都会带来自己的独有的剪枝方法,以至于大家可能会对到底选用什么方法来实现神经网络的剪枝感到迷盲。
在这里,将以此为主题,对目前较为流行的神经网络剪枝方法作一个概述,着重强调训练过程中神经网络稀疏性的演变过程。
训练神经网络的基本框架是:训练、剪枝和微调,涉及1)训练网络2)按照剪枝结构和剪枝准则的要求,将需要修剪的参数设置为0(这些参数之后也无法恢复),3)添加附加的epochs训练网络,将学习率设为最低,使得神经网络有一个从剪枝引起的性能损失中恢复的机会。通常,最后两步可以迭代,每次迭代均加大修剪率。
具体剪枝方法如下:按照权重大小剪枝原则,在剪枝和微调之间进行5次迭代。实验表明,通过迭代可以明显提高训练性能,但代价是要花费额外的算力和训练时间。这个简单的框架是许多神经网络剪枝的基础,可以看作是训练神经网络的默认方法。
有一些方法对上述经典框架做了进一步的修改,在整个训练过程中,由于删除的权重越来越多,加速了迭代过程,从而从迭代的优势中获益,与此同时,删除整个微调过程。在各个epoch中,逐渐将可修剪的过滤器数目减少为0,不阻止神经网络继续学习和更新,以便让它们的权重在修剪后能重新增长,同时在训练中增强稀疏性。
最后,Renda等人的方法指出:在网络被修剪后进行重新再训练。与以最低学习率进行的微调不同,再训练采用与原先相同的学习率,因此称这种剪枝方法为“学习率重绕”。这种剪枝后再一次重新训练的方法,比微调网络的性能更优。
为了加快训练速度,避免微调,防止训练期间或训练后神经网络架构的任何改变,许多工作都集中在训练前的修剪上:斯摩棱斯基在网络初始化时便对网络进行修剪;OBD(Optimal Brain Damage)在对网络初始化剪枝时采用了多种近似,包括一个“极值”近似,即“假设在训练收敛后将执行参数删除”,这种方法并不多见;还有一些研究对这种方法生成掩码的能力提出了保留意见,神经网络随机生成的每一层的掩码具有相似的分布特性。
另一组研究剪枝和初始化之间关系的方法围绕着“彩票假说”展开。这一假设指出,“随机初始化的密集神经网络包含一个初始化的子网,当隔离训练时,它可以在训练相同次数迭代后匹配原始网络的测试精度”。项目实践中,在刚刚初始化时,便使用已经收敛的剪枝掩码。然而,对这一剪枝方法的有效性,还存在着诸多质疑,有些专家认为,利用特定掩码来训练模型的性能甚至可以优于用“胜券”假设下获得的性能。
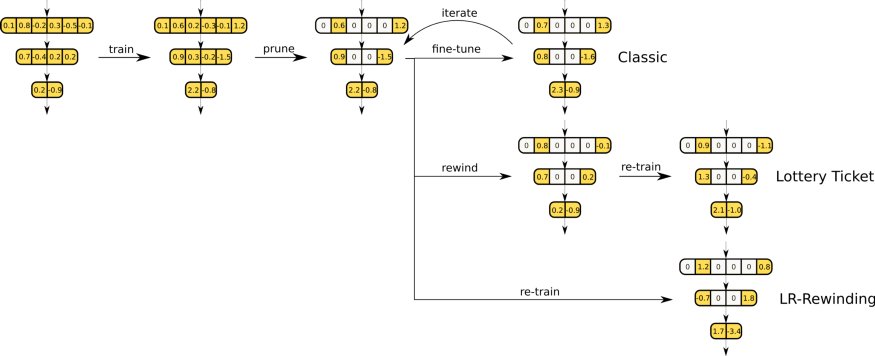
经典的剪枝框架、彩票假说的学习率调整比较
上述方法均共享相同的底层主题:在稀疏性约束下的训练。这一原则以一系列稀疏训练方法为核心,它包括在训练分布变化的情况下,执行恒定的稀疏率并逐步调整。由Mocanu等人提出,它包括:
1)用一个随机掩码初始化网络,并对网络进行一定比例的修剪
2)在一个epoch内训练这个修剪过的网络
3)修剪一定数量较小的权值,4)再生相同数量的随机权值。
这种情况下,剪枝掩码是随机的,被逐步调整以瞄准最小的导入权值,同时在整个训练过程中强制执行稀疏性。各层或全局的稀疏性级别可以相同。

稀疏训练在训练过程中周期性期切割和增长不同的权重,经过调整后的权重与相关参数的掩码相关
还有一些方法侧重于在训练期间学习掩码修剪,而不是利用特定准则来修剪权重。在这一领域,比较流行的有以下两种方法:1)对网络或层分开进行掩码学习,2)通过辅助参数进行掩码学习。第一种方法中可以采用多种策略:尽可能多的修剪的每层的过滤器,在最大限度地提高精度的前提下,插入基于attention的层或使用强化学习。第二种方法将剪枝视为一个优化问题,它倾向于最小化网络的L0范数和监督损失。
由于L0是不可微的,有些方法主要围绕着使用辅助的惩罚参数来实现,在前向通路中,将辅助的惩罚参数乘以其相应的参数来规避这个问题。还有一些方法采用了一种类似于“二进制连接”的方法,即:在参数选择时,应用随机门的伯努利分布,这些参数p利用“直接估计器”或其他学习方法获取。
有许多方法应用各种惩罚来增加权重,使它们逐步收缩为0,而不是通过手动修剪连接或惩罚辅助参数。实际上,这一概念相当古老,因为权重衰减是衡量权重大小的一个基本标准。除了单独使用重量衰减之外,还有许多方法专门为执行稀疏性而设计了惩罚。当前,还有一些方法在权重衰减的基础之上应用不同的正则化,以期进一步增加稀疏性。
在最近的研究中,有多种方法采用了LASSO(最小绝对收缩并选择操作符)来修剪权重或组。某些其他的方法还采用了针对弱连接的惩罚,以加大保留参数和修剪参数之间的距离,使它们对性能的影响降为最小。经验表明,在整个训练过程中进行惩罚,可以逐步修剪参数,从而达到无缝剪枝的目的。
在神经网络的训练过程中,无须从头开始实现(重用论文作者提供的源代码),在某些现成框架上应用上述基本剪枝方法,实现上相对会更加容易一些。
Pytorch为网络剪枝提供了多种高质量的特性,利用Pytorch所提供的工具,可以轻松地将掩码应用到网络上,在训练期间对该掩码进行维护,并允许在需要时轻松地恢复该掩码。Pytorch还提供了一些基本的剪枝方法,如全局或局部剪枝,无论是结构化的剪枝还是非结构化的剪枝,均能实现。结构化剪枝适用于任何维度的权值张量,可以对过滤器、内核行,甚至是内核内的某些行和列进行修剪。这些内置的基本方法还允许随机地或根据各种准则进行剪枝。
Tensorflow的Keras库提供了一些基本的工具来修剪权重较低的参数,修剪的效率根据所有插入的零引入的冗余来度量,从而可以更好地压缩模型(它与量化很好地结合)。
Blalock等人研发了一个自定义库ShrinkBench,以帮助社区剪枝算法进行规范化。这个自定义的库基于Pytorch框架,旨在使修剪方法的实现更加容易,同时对训练和测试条件规范化。它为不同的剪枝方法(如随机剪枝,权重大小剪枝或梯度大小剪枝),提供了不同的基准。
综上所述,可以看出
1)剪枝结构定义了通过剪枝操作可以获得哪种收益
2)剪枝准则基于多种理论和实际的结合
3)剪枝方法倾向于围绕在训练过程中引入稀疏性以协调性能和成本。
此外,尽管神经网络的基础工作可以追溯到上世纪80年代末,但是,目前神经网络剪枝是一个非常动态的领域,期待有新的基础理论和新的基本概念出现。
尽管目前该领域百花齐放,但仍有很大的探索和创新空间。每种剪枝方法都试图回答一个问题(“如何重建修剪后的权重?”“如何通过优化学习修剪掩码?”“如何释放已经剪去的权重……”),上述所有的研究指明了一个方向:贯穿整个训练过程中的稀疏性。同时,这一方向带出了许多新的问题,比如:“剪枝准则在还没有收敛的网络上有效吗?”, “如何判断是否剪枝选定的权重会有益于所有稀疏的训练?”
网格搜索类,群体优化算法类,强化学习类,梯度下降类
Introducing some second-order methods.
Given unconstrained, smooth convex optimization

where is convex, twice differentiable, and
.
1.chooses initial .
2. repeats

where is the Hessian matrix of
at
.
Newton's method needs not converge. This is because pure newton's method is not guaranteed to be a descent method.
Newton's method uses a better quadratic approximation of at
:
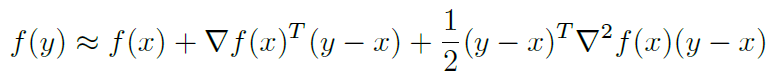
and minimizes over to yield the update rule

Taking the step in the newton direction but a scaled version of that; guaranteeing that the criterion
value decreases - ensuring descent.

The step size is chosen by backtracking line search.
We use parameters and
. At each outer iteration, we start with
and run an inner loop :

Log Barrier Function
The intuition is to try to push the inequality constraints into the criterion in a smooth way and only be left with equality constraints.
Consider the convex optimization problem:

Assume that are convex, twice differentiable, each with domain
(this last condition is just for simplicity).
We de fine the log-barrier function for the above problem as:

The domain for the above function is the set of strictly feasible points . We assume that this is non-empty - which, by using slater's condition, implies that strong-duality holds.
Now, consider the non-smooth exact transition of inequality constraints to the criterion:

The main idea is to try to approximate the indicator function using the log-barrier function as:

where is a large number. Note that the approximation becomes more accurate as
becomes larger.

Central Path
Using the log-barrier approximation, we have reduced our original problem to the barrier problem given as:

The central path is de ned as the solution as a function of
.
We now discuss a bunch of observations about this formulation:
- We do this with the hope that as
.
- We take a path instead of simply solving the problem for a very large value of
because of two issues
with using a large valued :
- Numerical instability
-Empirically, it leads to Newton method taking many iterations to reach the quadratic convergence
phase.
- Therefore, in both practice and principle it is much more effcient to traverse the path by solving this
problem for a bunch of intermediate values of , and use the solution for one value of
as warm start
for solution to next larger value of .
- Informally, it is always keeping Newton's method in the quadratic convergence phase.
The central path is characterized by its KKT conditions:

for some .
Barrier Method Algorithm
We solve a sequence of optimization problems:

for increasing values of . We stop when
, since duality gap is upper bounded by
.
Concretely:



Requirements for
- Secant Equation
Let ,
, the condition is:
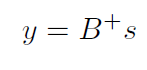
is symmetric
is "close" to
positive defi nite
positive de finite
BFGS update

DFP update

Broyden Class update






